RNG with USRP

This is completely open for comment, so if you have any thoughts on the quality of this Random Number Generator please contact me.

Introduction

It is possible to use a USRP to generate a stream of random numbers (i.e. an entropy generator). It relies on sampling the electrical & thermal noise in the Analog-to-Digital Converter, and converting this into a random bitstream.

All you need is:

• a bare USRP

  It is better to rely on the ADC alone, and avoid any signals introducted by a daughterboard (a signal may introduce repetition or 'structure' into the sampled signal and will therefore decrease the randomness or entropy of the generated bitstream).

• GNU Radio to sample, process and output the ADC data

WARNING: The following are the results from a completely ad-hoc experiment. Do not use this technique to generate entropy that will be used for anything that requires the slightest bit of security. Sample at your own risk! If you require something more secure, please learn about some Bruce Schneier Facts.

To use the Fast Auto-correlation block, you'll need to install gr-baz.

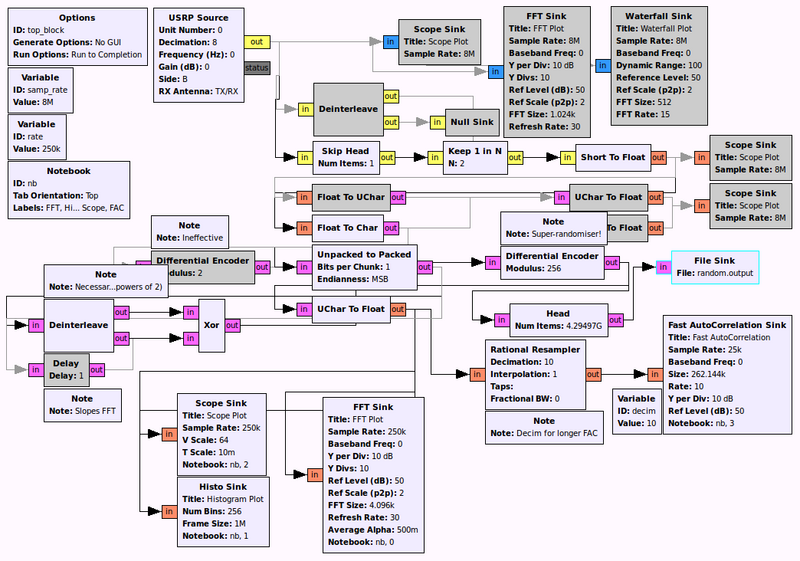
Flow-graph

GNU Radio Companion flowgraph implementation

Data flow consists of:

1. a USRP Source with gain 0 at maximum sample rate (here 8 Msps) outputting interleaved signed shorts

   The gain is set to zero to surpress any harmonics or spurious signals that may creep in (even though the input to the ADC is essentially disconnected). Raw samples (signed shorts) are output to avoid any rounding issues caused by type conversion (the default output type is floating-point complex samples).

2. extracting only one stream from the ADC

   Here the in-phase (real) samples are kept and quadrature-phase (imaginary) samples are discarded so that we only rely on a single signal path and ignore any variability between the I/Q paths

3. convert the real signed shorts to signed chars (bytes)
   • signed shorts -> float (direct value assignment & no scaling via gri_short_to_float)
   • float -> signed char (values are clamped in char range by gri_float_to_char)

     Note: even though the function performs clamping, actual values in this experiment will not be clamped because the value of the noise (low-level/weak signal) will always been between -128 and 127 (the valid range a signed char can represent). If values would be outside this range, and would therefore become clamped, this would likely affect the quality of the generated random bitstream.

4. the Least Significant Bit of each signed byte is extracted, and eight of these LSBs are used to form a new 'noisy' byte

   The LSBs of eight incoming bytes are re-packed to form a new 'noisy' byte that should be made up of the most 'noisy' (frequently changing) bit in the ADC samples

5. each pair of 'noisy' bytes are XOR'ed with each other

   The sampled noise signal will have a tendency to pass through particular values in a very small range (e.g. -4 to 4), and the distribution of those values will likely not be uniform. The 'noisy' bytes are effectively made up of whether the sampled ADC value was even or odd, since its (binary) LSB is sampled. This will introduce structure into the output random stream by distrupting the uniform distribution of the random values. To overcome this, the XOR operator is applied to each pair of 'noisy' bytes (XOR is a good operator to introduce more entropy). This can be thought of treating the first 'noisy' byte as an actual random value and the second as the value whose bits will flip the first's to ensure they won't be the same.

6. the XOR'ed 'noisy' bytes are then fed into mod 256

   The mod operator acts as a differential encoder so that we end up outputting the 'modded' distance between the current and previous XOR'ed 'noisy' byte values (continually moving about a circle at seemingly random intervals). Modulus 256 is chosen so that the output will already occupy all possible bits of each generated byte.

This can now be treated as the final random bitstream.

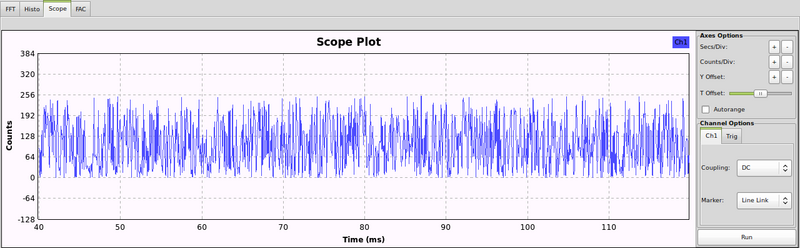
Results

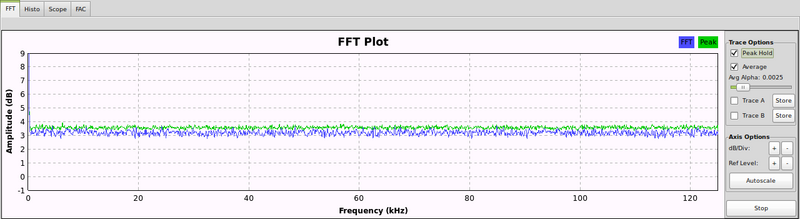
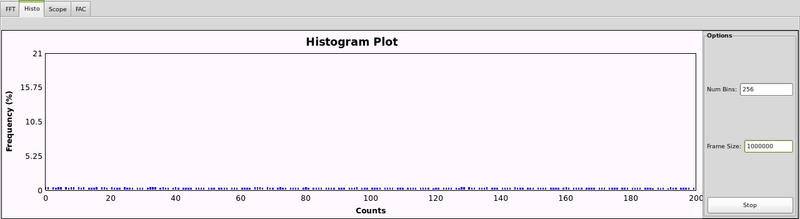
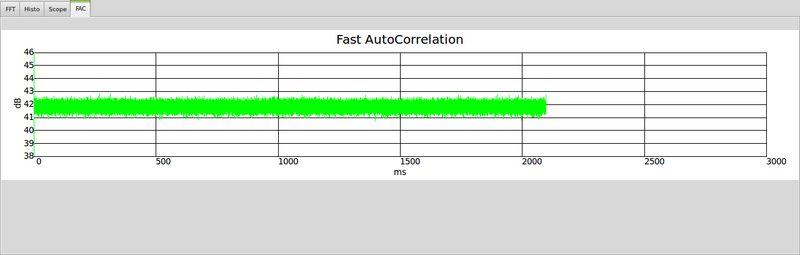
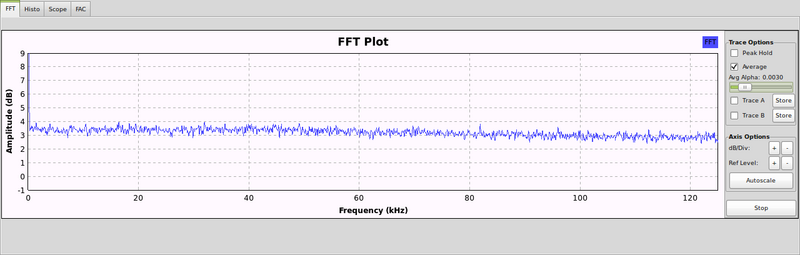
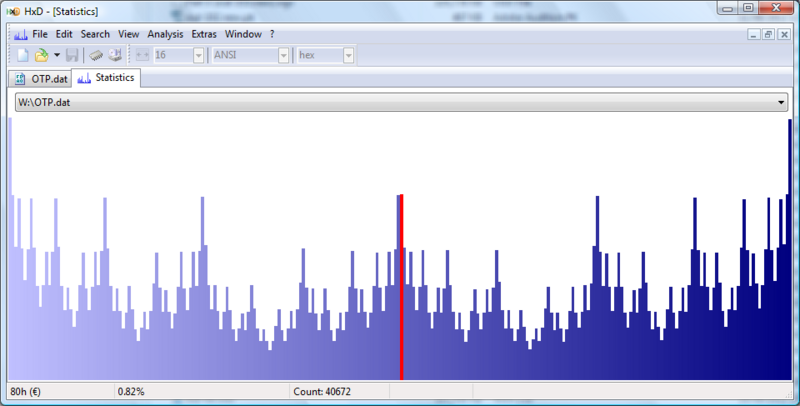
The final random bitstream appears to be 'pretty random':

Averaged FFT showing uniform distribution of energy (notice small amplitude scale)

Histogram showing uniform distribution of output bytes

Auto-correlation of random output over two second period. Even with small amplitde scale, no distinct peaks are visible suggesting there are no repeating components.

Scope plot of output bytes to check for any obvious patterns (not nearly as useful as the above analyses)

Byte-oriented histogram of the final (~3 MB) output stream showing uniform distribution

Issues

During development of the data flow, some problems were encountered.

Hint: In the following section, keep in mind that a re-packed 'noisy' byte, and a final output byte are a sequence of either binary digits that have been individually sampled earlier from the LSB of the ADC. Therefore each individual 1 or 0 can be thought of having been processed in sequence (they just happen to be packed into bytes as it is convenient, which means we look at the distribution of values between 0 and 255).

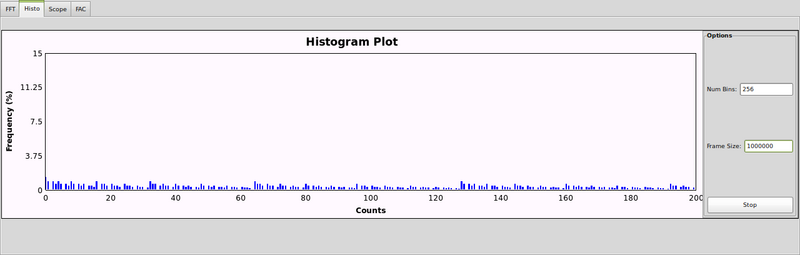
In the first iteration there was no XOR'ing or modulus applied. Even though the other analyses (above: FAC, FFT, scope) appeared uniform, the histrogram showed a slight non-uniformity. Upon closer inspection (especially in the histogram of the final output), it is clear that even numbers, and especially powers of two, are being favoured. In the 'space' between each successive occurence, one can observe an overall decrease in probability. This is clearly due to a non-uniform distrubtion of 1s and 0s in the 'noisy' byte (there is a greater chance of a 0 being selected over a 1). Also, the LSB from the raw ADC data (that is re-packed to form the 'noisy' byte) also tends to be 0 (explaining the greater amount of even numbers), which is reasonable to expect given the nature of the input signal (i.e. noise). In addition, the overall decrease in probability for higher values suggests that the more significant bits in the re-packed 'noisy' byte tend to be zero, and the less significant ones are randomly 1 or 0.

The XOR'ing pairs of re-packed 'noisy' bytes helped alleviate this issue.

Histrogram looks roughly uniform at first glance, however there is subtle skew and certain 'special' numbers occur more frequently than others

Histogram as above, but of final output bit stream, where the 'special' numbers are more pronounced

Although some tweaking appeared to help the previous issue before the XOR as applied, a second problem because apparent: a slight non-uniform distribution of energy in the FFT. Whether this is of any major significance is open for discussion.

Slight decrease in energy toward the right

In an attempt to overcome the first problem above, a differential encoder (mod 2) was added prior to the re-packing of the LSB of ADC samples into the 'noisy' byte. The purpose was to apply the modulus operator to the LSB because it had a tendency to pass through particular values in a very small range (due to the sampled noise). Applying mod 2 to the entire sampled byte was sufficient as only the LSB is of interest, and it would serve to smooth the aforementioned non-unformity, thereby increasing the bit's entropy.

However, this had an unintended and negative effect:

Mirrored distribution about the midpoint favouring powers of two

A byte of all 1s or all 0s are favoured equally, and then (equally, but with less probabilty than before) one less than powers of two up to 127, after which the distribution is mirrored. Application of mod would have generated more extended sequences of 1s and 0s, therefore bringing about the patterns of numbers just described that led to this worrying distribution.